Система уравнений алгебра как решить 8 класс. Алгебраический метод решения системы уравнения

Поиск решения системы уравнений подразумевает одновременное определение неизвестных, которое будет приемлемо для обеих уравнений. Переменные находят с помощью нескольких способов: подставления (замены), вычетания и графическим методом. Рассмотрим каждый из вариантов более подробно.

Как решать систему уравнений с 2 неизвестными

Данная система подразумевает под собой два уравнения, объединенных фигурной скобкой и записанных друг под дружкой. Например,

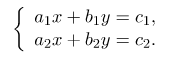
где а,b,c –заданные числа, а х,у- неизвестные.

Чтобы решить систему, необходимо определить значение неизвестных или доказать, что ответа не существует. Наиболее известные способы решения – это нахождение х,у методом подставления, вычитания и с помощью визуального графического метода.

Школьники или их родители, которые хотят проверить правильность решений подобных заданий, могут найти в интернете специальный онлайн калькулятор. Достаточно ввести на сайте уравнения и сервис сам рассчитает решение двумя методами. Причем, ответ получается пошаговый.

Для примера введем в отведенные графы уравнения.

В ответе получаем два пошаговых решения системы.

Как решить систему уравнений способом алгебраического сложения

Чтобы упростить подсчеты и сэкономить время поиска ответа достаточно применить алгебраический метод сложения. Суть данного способа поиска ответа заключается в избавлении от одной переменной.

Рассмотрим данный метод на простом примере.

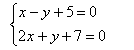
Сделав анализ системы, можно отметить, что переменная у имеет одно по модулю число, но с противоположным знаком (-1,1).

Сложим два уравнения почленно:

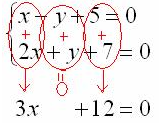
В результате действий переменная у пропадает.
Теперь осталось решить уравнение: 3х+12=0; х=-4.
Найдя переменную х, можно подставить ее в любое из уравнений.
-4-у+5=0; у=1.

Решение должно иметь следующие записи:

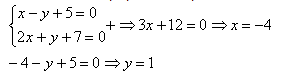Ответ: х=-4, у=1

Важно! При выражении переменной в ответе можно получить дроби, что значительно усложняет решение, а метод сложения исключает вероятность ошибки.

Рассмотрим еще один более сложный пример.

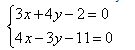
При анализе уравнений видим, что обе переменные имеют разные числовые коэффициенты. Если их сложить, то избавиться от неизвестной не получится.

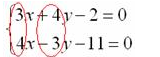
Для нахождения одинаковых по модулю чисел в парах, найдем их наименьшее кратное. Рассмотрим числовые коэффициенты при переменной х:

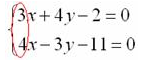
Наименьшим кратным является число 12. Числовые коэффициенты первого уравнения умножим на 4, а второго — на 3.

Важно! На определенное число умножается не только коэффициент неизвестной, но и каждый член уравнения.

Получаем:

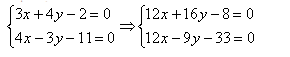
Затем вычтем из первого уравнения второе. Ниже приведен наглядный пример вычитания.

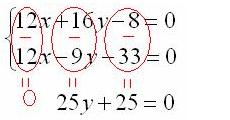
Запишем решение:

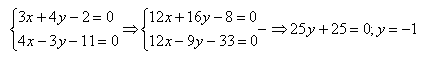
Найдя у, подставим ее в уравнение: 3х-4-2=0; х=2

Ответ: х=2, у=-1

Как решить систему уравнений методом подстановки х, у

Метод подстановки, который называют «школьным методом», предусматривает исключение одной неизвестной.

Способ имеет следующую последовательность:

1. нахождение одной переменной через другую;
2. подстановка значения и решение другого уравнения;
3. нахождение второй переменной.

Пример 1

Для начала свободные члены перенесем влево, не забывая сменить знаки.

Найдем х через у: х=у-5 и подставим это значение во 2-е уравнение:

2(у-5)+у+7=0
2у-10+у+7=0
3у-3=0
3у=3
у=1

Затем определимся со второй неизвестной х: х=1-5=-4

Ответ: х=-4; у=1

Во время решения можно изначально выражать любую переменную.

Как решать систему уравнений графическим способом

Метод предусматривает графическое определение общих точек пересечения графиков. Система может иметь одно решение в случае пересечения прямых, несколько решений — при графике из параллельных прямых и множество  решений — при совпадении графиков.

Пример 1 

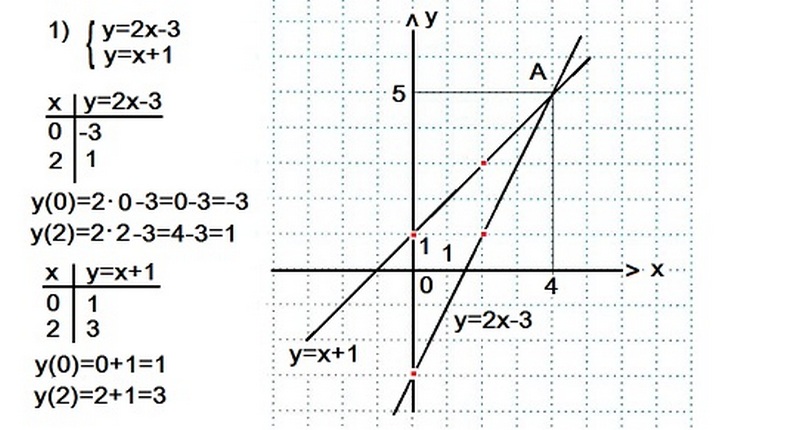
Для начала определимся с координатами х;у и нарисуем прямые. Функции имеют общую точку А (4;5), что будет решением системы.

Ответ: х=4; у=5

Пример 2

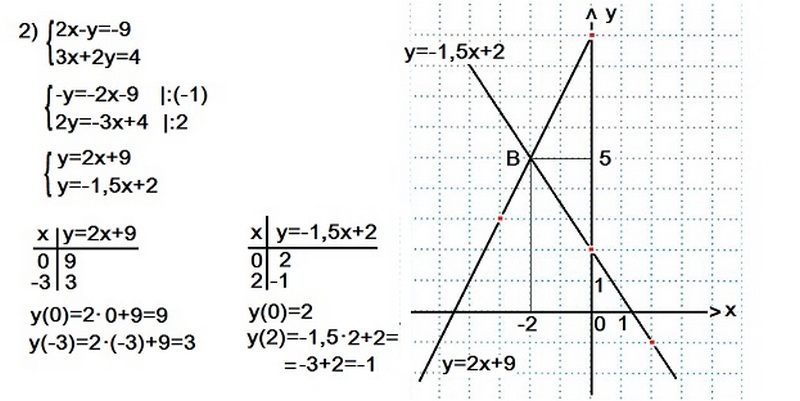
Чтобы решить второй пример необходимо выразить у через х, а затем определить точки прохождения прямых. Графики уравнений пересекутся в точке В (-2; 5).

Ответ: х=-2; у=5

Пример 3, где решений у системы нет.

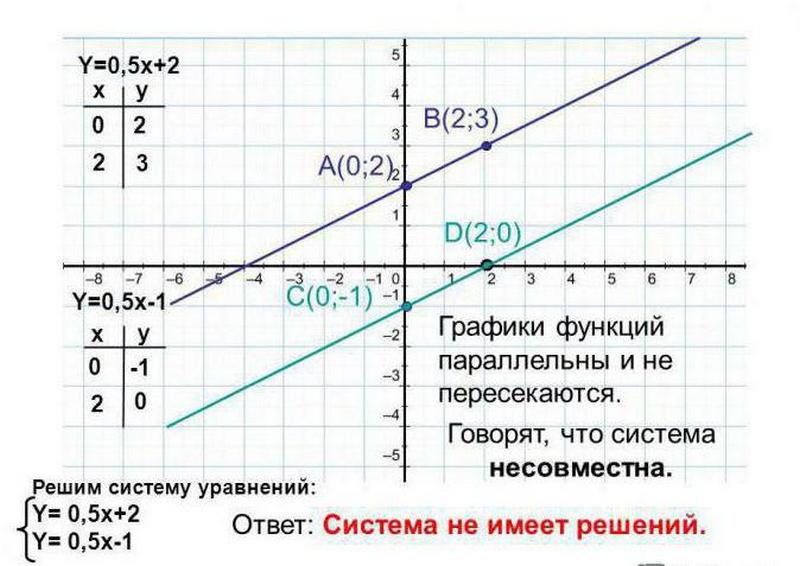
Последний графический способ считается неточным и системы с квадратами и корнями им не решить.

Если следовать алгоритму и верно выполнять все действия, можно с легкостью решить самые сложные системы уравнений.