Домашнее задание не так страшно, когда знаешь, как его объяснить ребенку. При чем, объяснение должно быть таким же, как и в школе. Иначе, вы будете объяснять по своему, а учитель по последним требованиям. Дроби, вопрос довольно не простой. И тут самое главное изначально разобраться, что за чем слагается, и в какой последовательности. Если знать эти тонкости, тогда и сложности вовсе никакой нет.
Содержание статьи
- Обыкновенные дроби 5 класс объяснение темы, кратко и понятно
- Видео обыкновенные дроби
- Правильные и неправильные обыкновенные дроби 5 класс, кратко и понятно
- Видео математика 5 класс правильные и неправильные дроби
- Правила сложения и вычитания дробей с одинаковыми знаменателями
- Видео математика 5 класс сложение и вычитание дробей с одинаковыми знаменателями
- Математика 5 класс дроби и деление натуральных чисел
- Видео математика 5 класс деление дроби на натуральное число
- Сравнение дробей 5 класс примеры
- Видео математика 5 класс сравнение дробей
Обыкновенные дроби 5 класс объяснение темы, кратко и понятно
Ребенку самому довольно сложно разобраться, что такое дробь, из чего она складывается. Поможет в этом банальный пример.

Главное, чтобы ребенок усвоил, что дробь, это часть чего-то целого.
Поясняем, например:
- Любимая шоколадка, это одна единица, значит 1.
- Конфета, тоже 1.
- Яблоко, тоже 1.
Если мы разделим например одну шоколадку на три равные части и возьмём одну часть, тогда получим от производной 1 три дроби. Записываем 1/3.
Наглядный пример на прямоугольнике и кружочках на нем. Если прямоугольник разделить на две части, тогда мы видим 1/2. Если на 4, тогда 1/4. Если на 8 частей, тогда 1/8.

У дробей есть циферка над и под черточкой. Над черточкой обозначается то что мы разделяем на части-числитель. Под черточкой, те части, которые мы выделили-знаменатель.
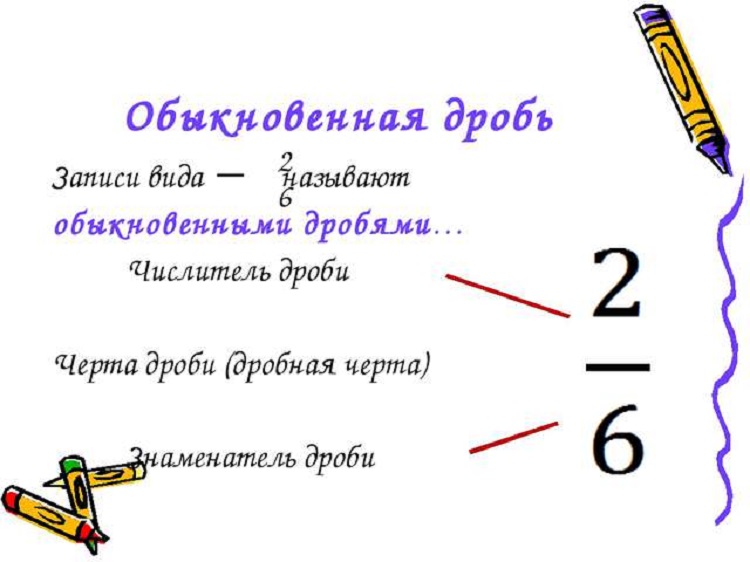
Чтобы проверить, насколько ваш ребенок усвоил базовое понятие, спросите у него:
Что обозначает циферка 7, в дроби 3/7.
- 7- количество частей, которые получили при делении.
Что обозначает циферка 3, в дроби 3/7.
- 3 — это три части от целого которое поделили на 7.
Видео ролик с пояснением
Видео обыкновенные дроби
Правильные и неправильные обыкновенные дроби 5 класс, кратко и понятно
Прежде чем приступать к разъяснению, необходимо усвоить самое главное:

Это азы, запомнив их, ребенок с легкостью сможет отличить правильное от неправильного.
Правильная дробь никогда не будет больше целого-единицы (1).

Неправильная же, может в процессе деления дать целое число, либо в верхней части (числителе) быть больше количества самих частей снизу.

Довольно часто неправильную дробь записывают так:

Если в конце решения примера мы получаем:

В примерах ребенок может встретить целое число, возьмем «2». Оно натуральное, предстанет в переводе неправильной дробью.

Если в примере есть два целых числа, их можно не переводить, просто сложить вместе.
Видео математика 5 класс правильные и неправильные дроби
Правила сложения и вычитания дробей с одинаковыми знаменателями
Для сложения дробей с одинаковыми знаменателями необходимо провести действие только в верхней части-над черточкой. Нижняя же часть-под черточкой остается не изменяемой.

Для вычитания дробей с одинаковыми знаменателями необходимо провести действие только в верхней части-над черточкой.Нижняя же часть-под черточкой остается не изменяемой.

Для смешанных дробей, имеющих одинаковую нижнюю часть под черточкой, изначально необходимо сложить целые числа в верхней части, затем в нижней.
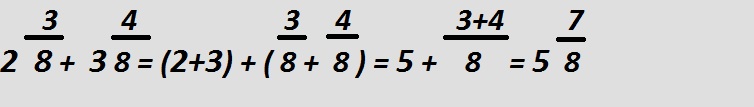
Если же у вас выйдет сумарно, в итоге, неправильная дробь, тогда необходимо выделить целое число и дробный остаток.
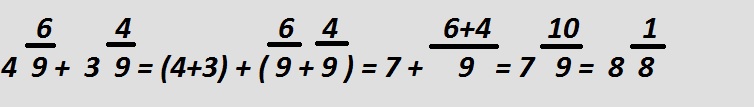
Для вычитания неправильных дробей необходимо провести те же манипуляции, что и для сложения. Все действия будут проходить только в верхней части дроби, над черточкой. Нижняя же часть останется неизменной.
Видео математика 5 класс сложение и вычитание дробей с одинаковыми знаменателями
Математика 5 класс дроби и деление натуральных чисел
Прежде чем приступить к пояснению, следует сделать акцент на понятии «натуральное число».
Натуральными считаются все числа от 1 и до бесконечности. Единственное условие положительность числа. Это значит, что оно не должно быть с «-«, например -2. Если мы видим минус, значит оно отрицательное. Дроби и числа со знаком «-» к натуральным не относятся.
Используя дроби можно выполнить запись деления двух абсолютно любых натуральных чисел.

Если в процессе мы получаем целое число, тогда оно будет натуральным. Если же целое число у нас не получается, тогда частное называется дробным.

Делим любое натуральное число

Если в примере есть одинаковая нижняя часть под черточкой, тогда она выносится за пределы скобок.
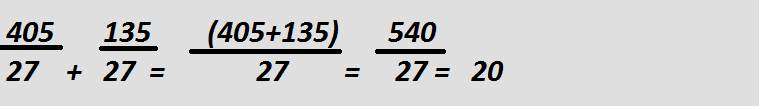
При делении суммы на какое-то число, мы можем отдельно провести деление каждой слагаемой суммы. В конце все части необходимо сложить вместе.
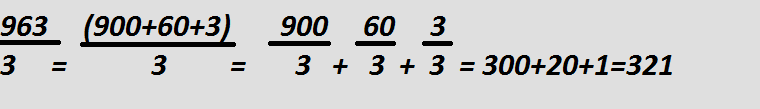

Видео математика 5 класс деление дроби на натуральное число
Сравнение дробей 5 класс примеры

Сравнивать дроби можно только в том случае, если они одинаковые. Если нет, нужно свести их сначала к общему числу под черточкой.
Когда сравниванию подлежат дроби с одинаковыми числами под нижней чертой, тогда соизмеряется их верхняя часть-доля.
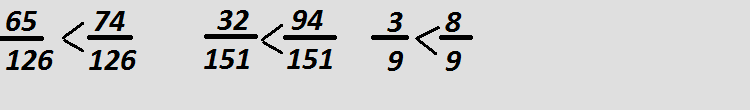
Когда сравниванию подлежат дроби с разными числами в нижней части под чертой, тогда нам необходимо найти одно общее число и свести к нему.

Видео математика 5 класс сравнение дробей
PS: Дроби совершенно несложные. Главное изучить правила, понять что над черточкой числитель, а под ней знаменатель, что мы делим и что называем делителем, что такое доли. Тогда с решением примеров у ребенка не будет абсолютно никаких сложностей.



