Неравенство — математическое действие, сравнивающее два выражения с помощью знаков больше или меньше. Многие простые неравенства решают путем сложений, вычитаний, умножений и делений сторон, а более сложные — методом интервалов.
Содержание статьи
Примеры уравнений неравенств
В алгебре такими неравенствами заменяют наборы решений, чтобы не перечислять большое количество чисел.
как читать неравенство
В неравенствах легко запутаться, поэтому их читают слева направо.
символ неравенства
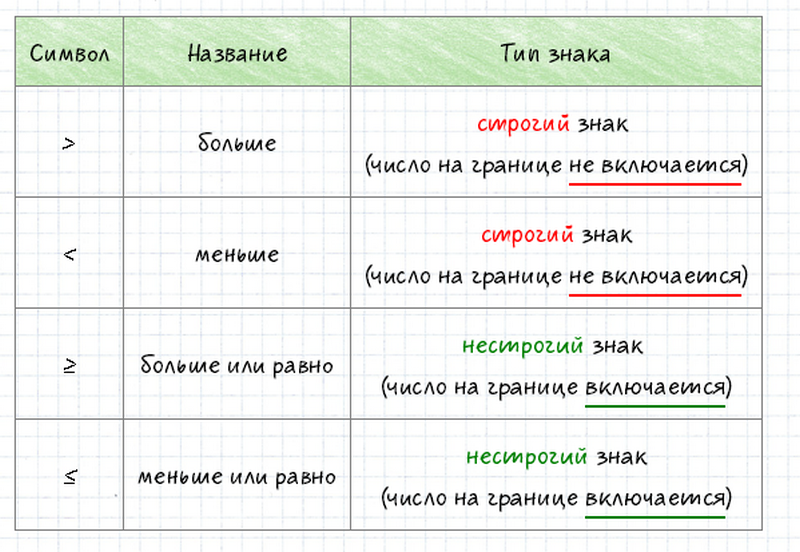
Неравенство х>у также можно записать как у<х. Стороны любого неравенства можно поменять местами при условии смены символов между ними.
верное и неверное неравенство
Числовое неравенство может быть:
верным: 18>7 и неверным: -5 >2,
строгое и нестрогое неравенство
строгими: х<21 и нестрогими: х≤47.
Неравенство с переменной (х,у) подразделяют на :
линейные неравенства с одной переменной
Линейные (1 степень переменной): 3х-5> 2(4-х)
квадратные неравенства примеры
Квадратное (квадрат переменной):
![]()
логарифмические неравенства 1
Логарифмическое (переменная под логарифмом):
![]()
показательные неравенства с переменной
Показательное (переменная в N-ой):
![]()
Методы решения неравенств примеры
Правила решения простых неравенств аналогичны правилам решения линейных уравнений.
правила решения неравенств
Чтобы решить неравенство, нужно:
- Добавить с обеих сторон одинаковое число.
- С обеих сторон вычесть одинаковое число .
- Умножить стороны на одинаковое положительное число.
- Разделить обе части на одинаковое положительное число.
- Умножить или разделить обе стороны на одинаковое отрицательное число и сменить знак в обратную сторону.
8 класс
решение неравенств графическим способом
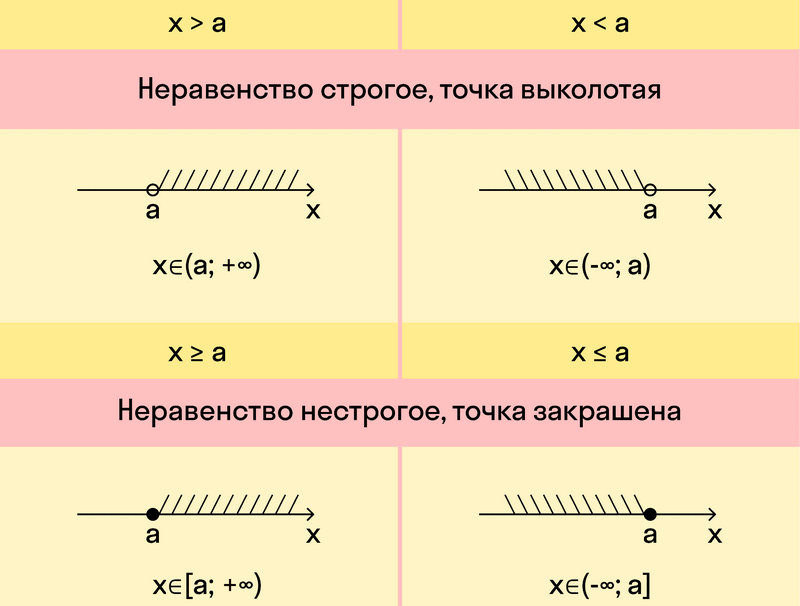
Графическое изображение неравенства
Неравенства нередко изображают на числовой прямой. Графики — очень полезный способ визуализации, особенно при бесконечном списке чисел.
1)х ≤ -4
Решением неравенства будут все действительные числа в числовой строке, которые меньше или равны 4.
Ответ: х ∈ [-∞;-4]

простые неравенства примеры решения
Решение неравенства с помощью сложения и вычитания
Когда добавляется или вычитается одно и то же значение с обеих сторон неравенства, неравенство сохраняется.
Если а > ба > б, то а+c > б+cа+c > б+c.
Если а > ба > б, то а-c > б-cа-c > б-c.
2) х + 3 < 5
Нужно найти такое значение х, которое при сложении с 3 будут меньше 5.
х+3<5
х+3-3<5-3
х<2
Ответ: х ∈ (-∞;2)
3) x-3+2 <10
Решение:
x-3+2 <10
x-1<10
x-1+1<10+1
x <11
Ответ: х ∈ (-∞;11)
4) р/5> 3
Решение:
р/5> 3
р/5•5>3•5
р>15
Ответ: р ∈ (15; +∞)
5) 12> 18-y
Решение:
18-y <12
18-y -18<12-18
-y <-6
y> 6 (не забудьте перевернуть символ при умножении на -1)
Ответ: у ∈ (6; +∞)
9 класс
дробные неравенства примеры решения
1) 2/3 р+4>10
Решение:
2/3 р+4-4>10-4
2/3р>6
2/3р • 3/2>6 • 3/2
р>9
Ответ: р ∈ (9; +∞)
2) (у-3)/2<−5
Решение:
(у-3)/2•2<−5•2 (каждую часть умножим на 2)
у-3 <-10
у-3 + 3 <-10 + 3 (с обеих сторон прибавим 3)
у <−7
Ответ: у ∈ (-∞; -7)
3) -2<( 6-2р)/3<4
Решение:
-2•3 < (6-2р)/3•3<4•3 (чтобы убрать дробь, умножим на 3)
-6<6-2р<12 (теперь вычтем 6)
-12<-2р<6 (разделим каждую часть на 2)
-6<-р<3 (умножим каждую часть на -1 и сменим направление знака)
6>р>- 3
Меньшее число переместим влево, большее — вправо. Поменяем их местами вместе со знаками.
-3<р<6
Ответ:-3<р<6 или р∈ (-3; 6)
4) 2 (8-p) ≤ 3 (p+7)
Решение:
2(8-p) ≤ 3(p + 7)
16-2p ≤ 3p + 21
16-21 ≤ 3p + 2p
–5 ≤ 5p
–1 ≤ p
p ≥ –1
Ответ: р ∈ [-1; +∞)
5) 4х^2-4х(х+5)≥80
Решение:
4x^2−4x^2−20x≥80 (упрощаем левую часть)
−20x≥80
x≥−4
Ответ: x ∈ (−∞;−4]
10 класс
неравенства 10 класс примеры с решением
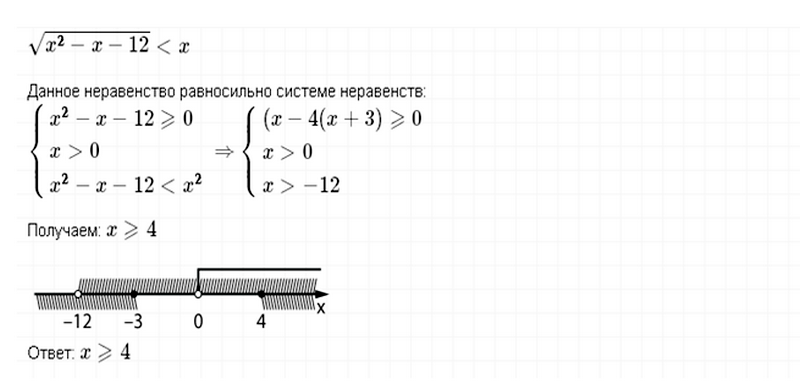
1)√3х+3≤6
Для начала необходимо найти ответ уравнения
√3√х+3=6
√3√х+3-3=6-3
√3√х=3 ( разделим обе стороны на √3)
√х=√3
х=3

Ответ: 0≤х≤3 или х ∈ [0; 3]
2)
3) (х-15)/(х+16) >2
Решение:
х-15-2(х+16)/х+16>0
(х-15-2х-32)/х+16>0
-х-47/х+16>0
-х-47=0
х=-47
х=-16
Нанесем точки на ось

Ответ : х ∈ (−47;−16)
4)

5)
Квадратные неравенства примеры
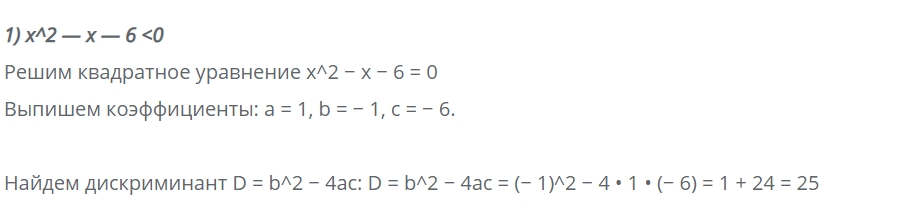
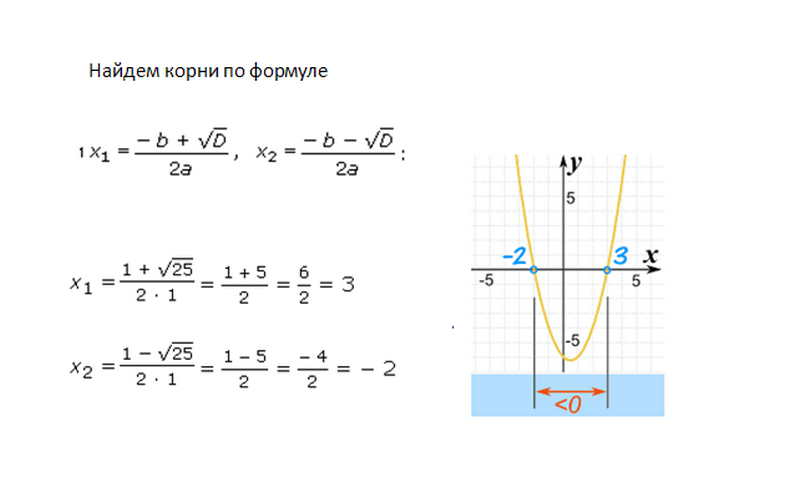
Ответ: x ∈ (−∞, −2) и (3, + ∞)
2) 4x^2 − 8x − 5 ≥ 0
Решим уравнение: 4x^2 − 8x − 5= 0
Выпишем коэффициенты: a = 4, b = − 8, c = − 5.
D = b^2 − 4ac = (− 8)^2 − 4 • 4 • (− 5) = 64 + 80 = 144
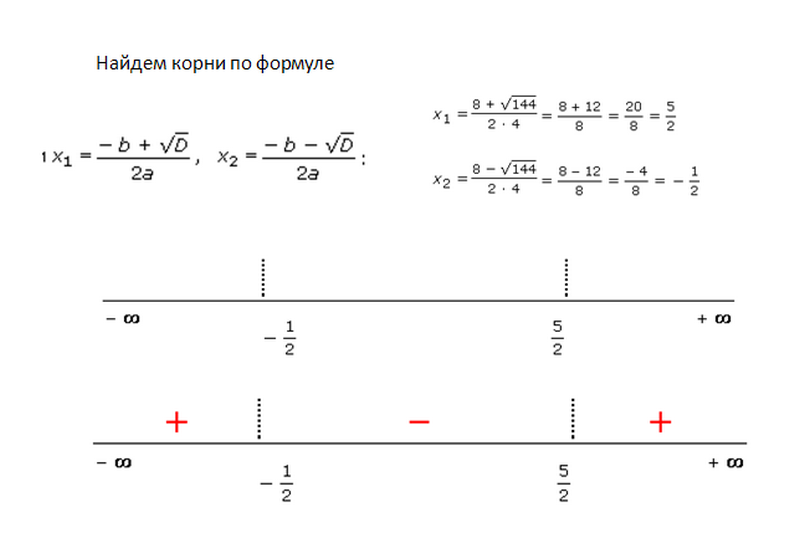
Данные корни разбивают числовую прямую на три интервала:
(-∞;-1/2], [-1/2;5/2], [5/2; +∞]
Определим знаки выражения 4x^2 − 8x − 5 на каждом из интервалов.
Руководствуемся следующим правилом:
- если при x^2 стоит положительный коэффициент, то знаки будут +, −, +;
- если при x^2 стоит отрицательный коэффициент, то знаки будут −, +, −.
В нашем случае при x^2 стоит положительный коэффициент 4, поэтому знаки будут +, −, +.
Поскольку знак неравенства «≥», то ответом будут те промежутки, на которых выражение 4x^2 − 8x − 5 принимает значения, большие или равные 0 (промежутки со знаком +).
Ответ: (-∞;-1/2] U [5/2; +∞]

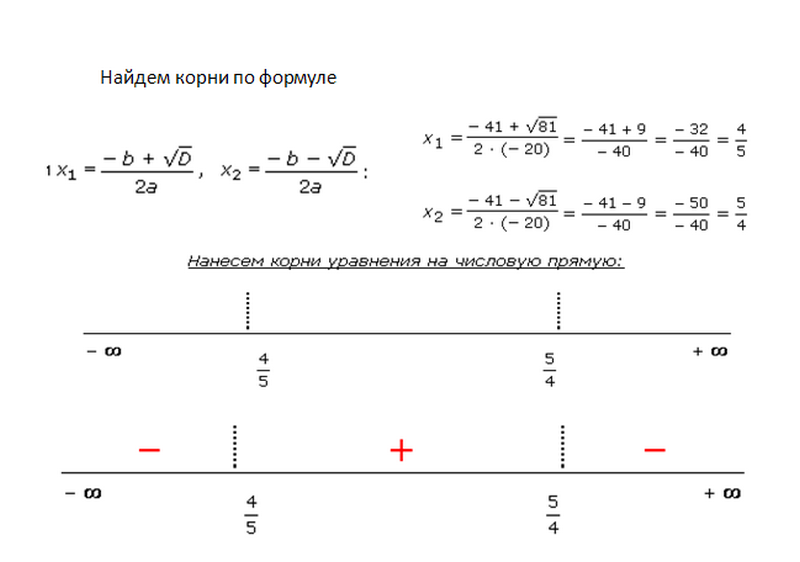

4) x^2−5x<6
Решим уравнение: x^2−5x−6=0 по теореме Виета:

Нанесем найденные точки на числовую ось и вычислим знаки на каждом интервале:
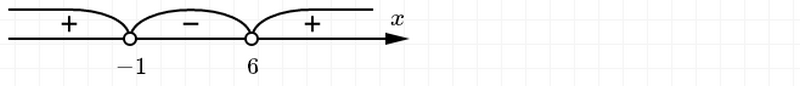
Ответ: x ∈ (-1;6) или -1<x<6
5) 4x^2+12x ≥−9
Решим уравнение 4x^2+12x+9=0
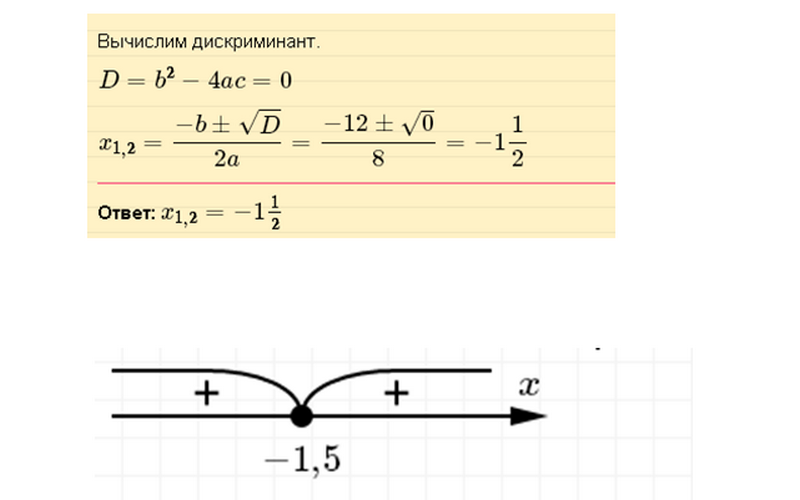
Ответ: x ∈ R или x — любое число.
Линейные неравенства примеры
1) 4x−7 ≤−9−4x
4x−7 ≤−4x−9
8x ≤−2
x ≤−1/4
Ответ: x ≤−1/4 или x ∈ (−∞;−1/4]
2) 2(7−3y)+4(8−y)≤60
В левой части раскроем скобки:
−6y+14−4y+32≤60
−10y+46≤60
−10y≤14
y≤−1,25
Ответ: y ∈ [−1,25;+∞)
3) 2(x+3)+2(−1)x≤3x+15
Упрощаем многочлен
−2x+2x+6≤3x+15
6≤3x+15
−3x≤9
x≤-3
Ответ: x ∈ [−3;+∞)
4)6<4x−16≤26
6+16<4x−16+16≤26+16 (прибавим 16)
22<4x≤42 (разделим на 4)
5,5<x≤10,5
Ответ : 5,5<x≤10,5 или x ∈ (5,5;10,5]
5)

Ответ: x ∈ (−∞;0,25)
Логарифмические неравенства примеры решения




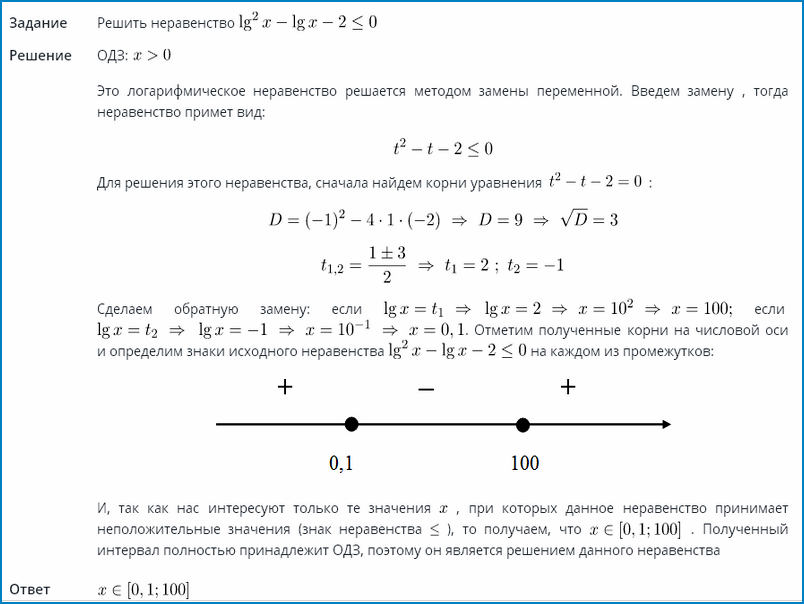
Решения неравенств методом интервалов примеры
Неравенства с дробью и степенью больше квадрата решают методом интервалов.




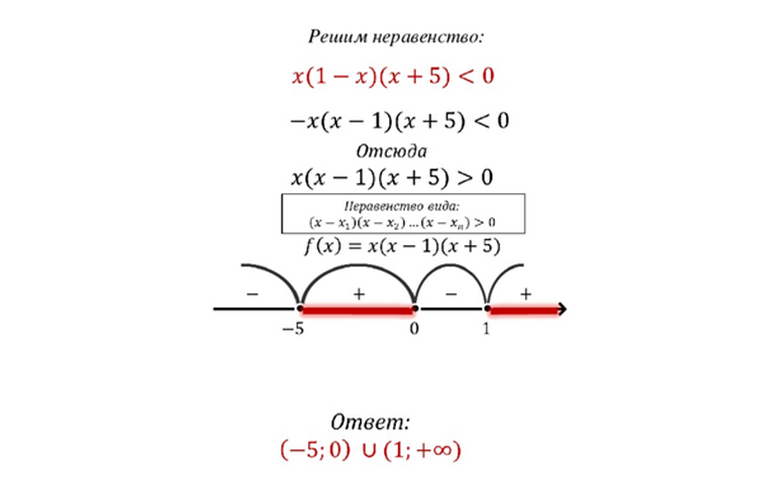
Методов решения неравенств несколько, поэтому важно применить наиболее подходящий способ для конкретного неравенства.



