У большинства школьников решение тригонометрических уравнений вызывает страх и панику. Как же разобраться в этих непонятных синусах, косинусах, arcsinах, когда возле них стоят неизвестные? Поверьте, не все так страшно как кажется на первый взгляд. Выбрав правильный метод решения, упростив уравнение, можно справиться с самыми сложными тригонометрическими заданиями.
Содержание статьи
Виды тригонометрических уравнений
Тригонометрическое уравнение — это равенство, при котором неизвестная величина входит под знак тригонометрической функции.
- 3sinx — 4cos x — tqx +1=0;
- sin4x+2sinx+1=0,
- sin2x + cos x=1,…
А вот такое равенство sin5x+4x=2 нельзя считать чисто тригонометрическим. Оно состоит из линейной (4х) и тригонометрической составляющей, поэтому относится к смешанному виду.
В тригонометрии различают простейшие и сложные тригонометрические уравнения:
- К первому виду относятся такие равенства, как sinf(x)=a, где под значением а подразумевают постоянное число (0,3,1,-1 и т.д.), а f(x) – функция, которая зависит от неизвестной х (f(x)=4, f(x)=6-х).
- Сложными примерами тригонометрических уравнений могут быть такие задания: (3sin x+ 4cos x)√2= tq x+ ctq x; sin x+ sin2 x+ cos2х=0 и т.п.
Решить такое уравнение – значит определить все значения неизвестной величины, которые оправдывают равенство.
Простейшие тригонометрические уравнения формулы
Простейшее тригонометрическое уравнение имеет одну неизвестную под знаком функции, которая равняется какому-либо числовому значению.
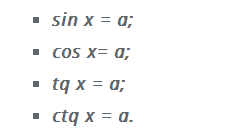
Найдем решение уравнений при значении а, в частности: а=0; а=1; а= — 1.
- Если sin x=0, тогда х=nπ. Синус равняется нулю для дуг, которые заканчиваются в концах горизонтального диаметра. Такое множество дуг выражается формулой х= nπ; n Є Z. (Здесь и далее n Є Z).
Если cos x=0, тогда х=π/2+ nπ. Косинус равен нулю для дуг, которые заканчиваются на концах вертикального диаметра. Множество таких дуг выражают формулой х= π/2+ nπ.
Если tq x=0, тогда х= nπ.
Если ctq x=0, тогда π/2+ nπ. - Если sin x=1, тогда х= π/2+2 nπ. Синус равен единице для дуг, которые оканчиваются в верхнем конце вертикального диаметра. Множество таких дуг выражается формулой х= π/2+2 nπ.
Если cos x=1, тогда х=2 nπ. Косинус равен единице, когда заканчивается в правом конце горизонтального диаметра. А множество таких дуг выражается формулой х=2 nπ. - Если sin x=-1, тогда х=- π/2+2 nπ, т.к. синус равен -1 для дуг, которые заканчиваются внизу вертикального диаметра. Множество таких дуг выражается с помощью формулы х=- π/2+2 nπ.
Если cos x=-1, тогда х=(2n+1)π. Косинус равен -1 для дуг, которые заканчиваются в левом конце горизонтального диаметра. Множество таких дуг выражается формулой х=(2n+1)π.
Для значений а, которые равны 0,1,-1, формулы решений простейших уравнений такие:
- если sinx = a(|a|≤1), тогда x = (-1)n arc sina + πn, n Є Z,
- если cosx= a(|a|≤1), x=± arc cosa +2nk, n Є Z,
- если tq x = a, тогда x = arc tq a + πn, n Є Z,
- если ctq x = a, тогда x = arc ctq a + πn, n Є Z.
Все значения тригонометрической функции имеют неограниченное количество углов, поэтому уравнение имеет множество решений.
Таблица тригонометрические уравнения
Нахождение переменной под функцией значительно упрощают специальные таблицы с расшифровкой основных формул.
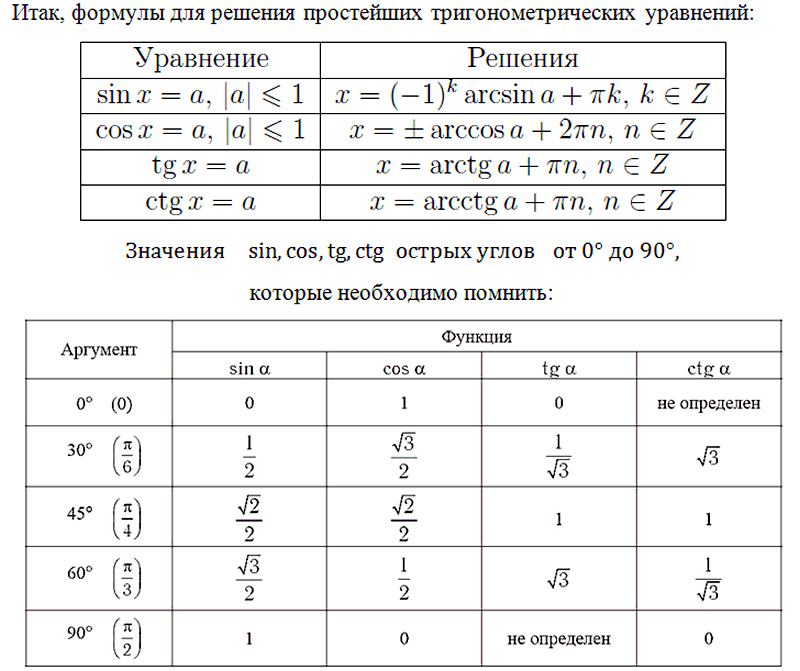
Решение тригонометрических уравнений формулы
Чтобы найти переменную под тригонометрической функцией, необходимо определить все величины, которые ее оправдывают. Такие уравнения не всегда имеют решение. Например, уравнение sinx=9, останется без ответа, т.к. абсолютная величина синуса не должна превышать единицу.
Обычно решений тригонометрических уравнений бесчисленное множество. Например, общим решением тригонометрического равенства sinx=0, будет х= nπ, где n Є Z, где Z — множество чисел.
Чтобы найти переменную в сложном тригонометрическом уравнении, его необходимо свести к простейшему. Для этого производят алгебраические преобразования, используя в решении тригонометрические формулы. Приведем общие решения некоторых уравнений.
Способы решений тригонометрических уравнений
Используя основные формулы, можно справиться с простейшими тригонометрическими уравнениями, а сложные равенства свести к простейшим. Для этого используют способы предварительного разложения левой части на множители, алгебраический метод (введения переменной), способ универсальной подстановки и др.
Пример решения, где использован метод разложения на множители
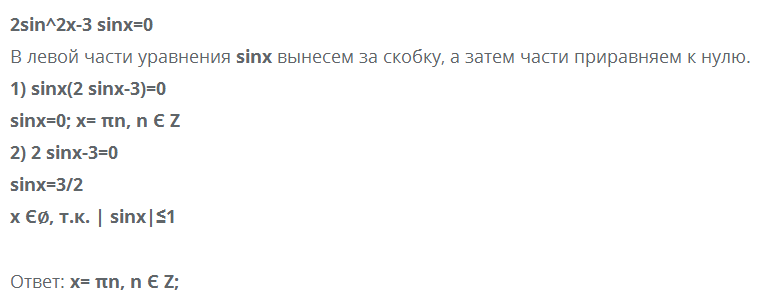Пример с введением переменной
Пример сведения к однородному уравнению
Тригонометрические уравнения ЕГЭ задания, с подробным решением 5 вариантов
В ЕГЭ тригонометрические уравнения встречаются редко, примерно в 7% случаев, но знать решение таких заданий просто необходимо. Предлагаем рассмотреть несколько подробных методов нахождения переменной.
Пример решения уравнения через главное тождество
Пример с использованием разложения
Пример решения этого же уравнения через деление на косинус
Пример решения уравнения через деление на косинус
Пример решения уравнения относительно аргумента
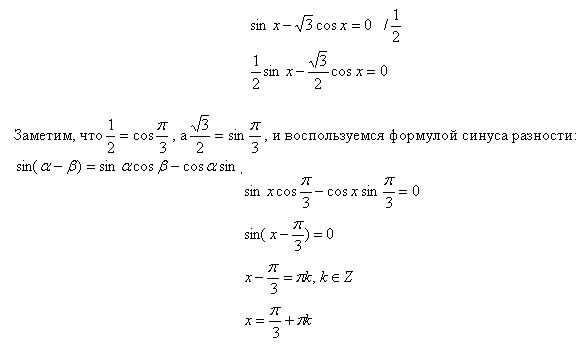
Зная основные формулы и методы решения, можно справиться с самыми сложными тригонометрическими уравнениями. Для самопроверки используйте онлайн калькулятор.
