Как узнать объём по размерам, формулы вычисления объема фигур, объёмы фигур ЕГЭ: цилиндра, куба, шара, параллелепипеда, пирамиды, конуса

Начиная с 5 класса, ученики начинают знакомство с объемными фигурами, которые окружают нас во внешней среде. Ученики изучают их свойства и учатся рассчитывать их объем. Чтобы было легче находить объемы различных фигур, предлагаем вам необходимые формулы и простые правила-подсказки.

Чтобы вычисление объема было несложной и увлекательной задачей, важно хорошо разбираться с базовыми определениями. Объем — характеристика пространства в количественном виде, которое занимает любое геометрическое тело. Иными словами, объем можно назвать определенным местом, которое занимает тело в представленном пространстве.

Объем измеряется в установленных единицах, например, в м³, а также в см³ или мм³. Полученная величина объема показывает нам то количество измерительных единиц, которые есть в данном теле.

Также важно помнить свойства объема тел:

• Если тела одинаковые, их объемы равны.
• Объемные предметы обязательно имеют свой объем. Например, всегда можно вычислить объем вазы, мяча, кровати.
• Если объемная фигура вмещает два и более тел, ее объем образуется из всех составляющих.

Формула расчета объема цилиндра

Рассчитать объем представленного цилиндра можно двумя способами, исходя из имеющихся данных:

объём через площадь основания и высоту

Первый вариант ― расчет объема через площадь и известную высоту фигуры. В данном случае объем цилиндра (обозначаем V) — произведение высоты и вместе с ней площади цилиндрического основания. Вид формулы: V=S*h.

Пример:

объём через высоту и радиус основания

Второй вариант ― расчет объема через высоту цилиндра и радиус его основы. Как известно, основания данной фигуры представлены кругом. Его площадь поможет рассчитать формула: S = ∏*R²

Исходя из этой формулы, легко находим объем: V = ∏*R²*h

Пример:

Как вычислить объем параллелепипеда формула

Любой многогранник, представленный шестью гранями в виде параллелограммов, правильно именовать параллелепипедом. Когда его грани — прямоугольники, фигура становится прямоугольным параллелепипедом. В зависимости от вида параллелепипеда используется удобная в конкретном случае формула.

Для того чтобы узнать объем параллелепипеда, прибегают к такой формуле:

объём параллелепипеда по площади основания и высоте

Пример:

Если требуется объем параллелепипеда прямоугольной формы, применяется формула такого вида:

объём параллелепипеда прямоугольной формы по длине, ширене, высоте

Пример:

Чему равен объем пирамиды формула

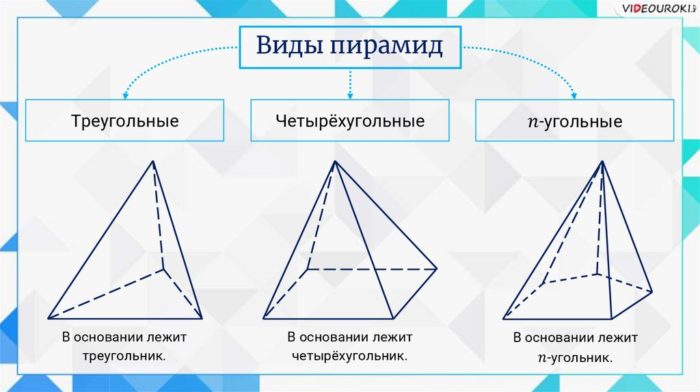
Любой многогранник, в основе которого многоугольник, а его грани — треугольники, именуется пирамидой. Рассчитать ее объем можно несколькими способами в зависимости от типа самой пирамиды.

Объем обычной пирамиды можно рассчитать по площади и высоте данного тела. Объемом в данном случае будет умножение трети площади на имеющуюся высоту: V=1/3*S*h.

формула объём пирамиды по площади основания и высоте

Пример:

Формула объема правильной четырехугольной пирамиды

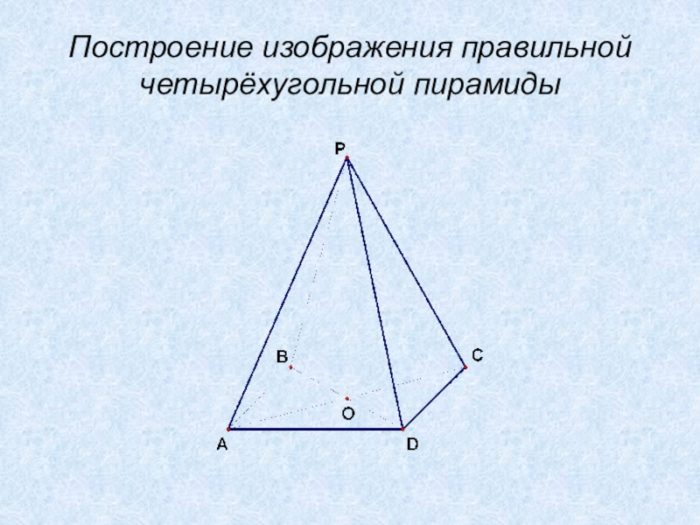
Объема четырехугольной пирамиды (ее особенность — основание-квадрат) определяется с учетом таких величин, как высота тела и сторона его основы:

Пример:

Формула объема шестиугольной пирамиды

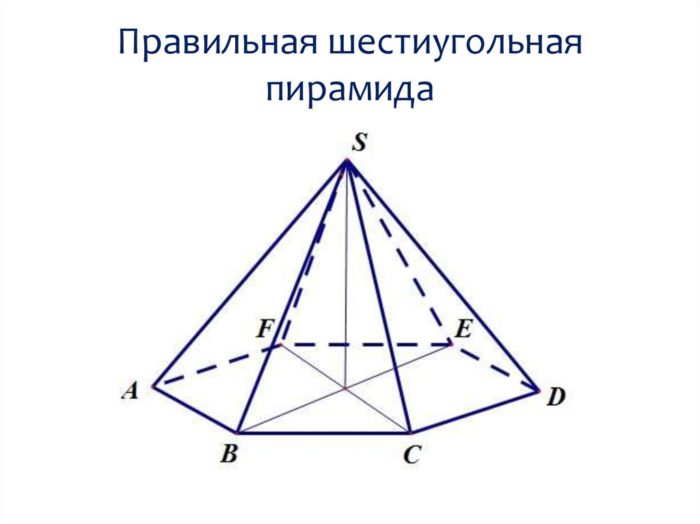
Многогранник, основой которого является правильный шестиугольник, а его грани формируют правильные треугольники, принято называть шестиугольной пирамидой. Она обладает особенными свойствами:

• Длина всех сторон ее основы всегда одинаковая.
• Углы, которые лежат в основе равные.
• Боковые грани обязательно имеют одинаковую площадь.

Чтобы рассчитать объем такой пирамиды, достаточно знать площадь основы и высоту фигуры:

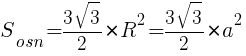
Теперь вернемся к формуле объема нашей пирамиды. Выглядит она так:

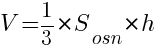
Пример:

Объем правильной треугольной пирамиды формула

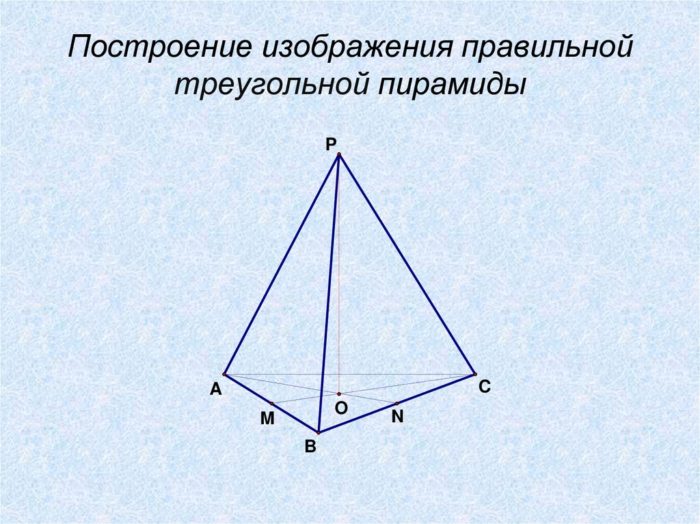
Если перед нами стоит задача посчитать объем треугольной пирамиды применяется следующая формула:

Пример:

Объем шара формула через радиус

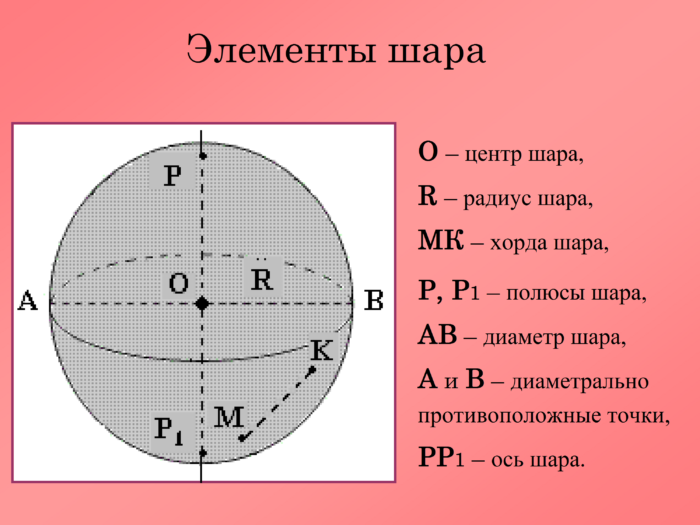
Объемная фигура, точки которой находятся от центра на расстоянии, которое не больше радиуса, принято называть шаром. При этом шар, точно так же, как и круг имеет диаметр, который вдове больше радиус шара. Для вычисления объема данной фигуры необходимо знать лишь радиус и число π.

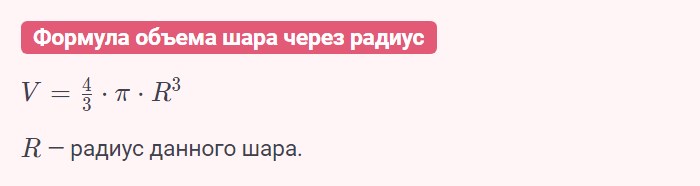
Пример:

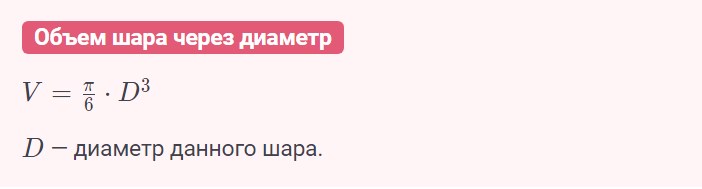
Объем шара формула через диаметр

Рассчитать объем шара можно через его диаметр. Для этого вспоминаем, что R=D/2. С помощью этой формулы находим радиус, а затем возвращаемся к базовой формуле и выводим несложную формулу в данном случае:

Пример:

Какие формулы объема куба

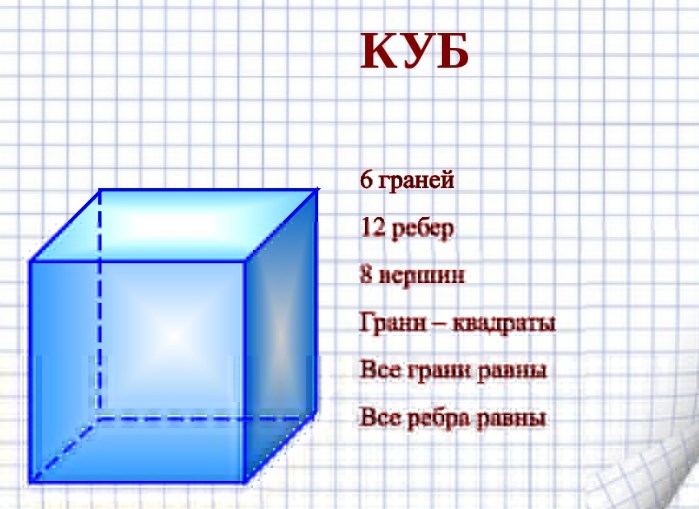
Куб ― фигура в виде правильного многогранника, многоугольники которого являются квадратами. Часто эту фигуру называют гексаэдром. Особенностью данной фигуры можно назвать наличие 12 ребер, 6 граней, а также 8 вершин.

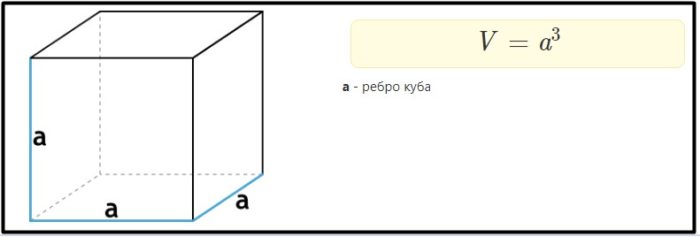
Объем куба через его ребро. Нахождение объема куба не составляет труда. Необходимо всего лишь умножить его измерения, под которыми имеются ввиду: ширина, длина, и, конечно же, высота. Помня о том, что куб состоит из нескольких квадратов, делаем выводы, что его измерения равны и соответствуют длине ребра.

Пример:

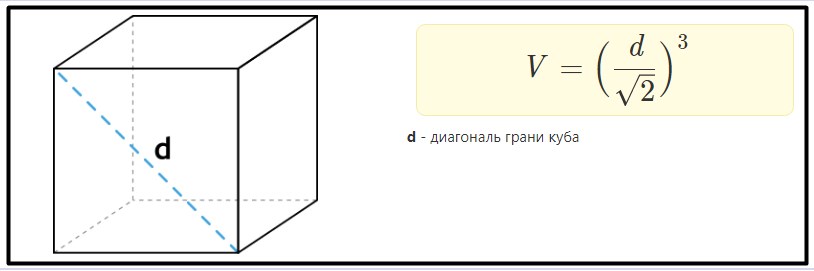
Объем куба через диагональ его грани. Факт, что грани куба равны и образуют квадрат, является доказанным. Поэтому вычислить сторону a через диагональ можно, используя формулу: a=d/√2. Исходя из этого, рассчитать объем поможет формула:

Пример:

Объем через периметр грани. Зная, что все стороны грани одинаковые, легко найти сторону а, разделив известный периметр на 4. Потом остается лишь возвести результат в третью степень.

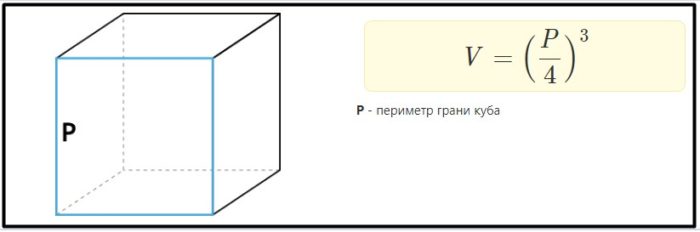
Пример:

Также есть две вспомогательные формулы расчета объема:

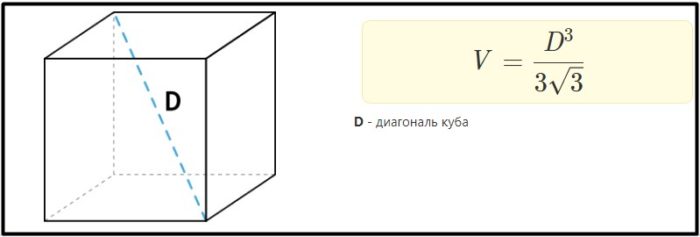
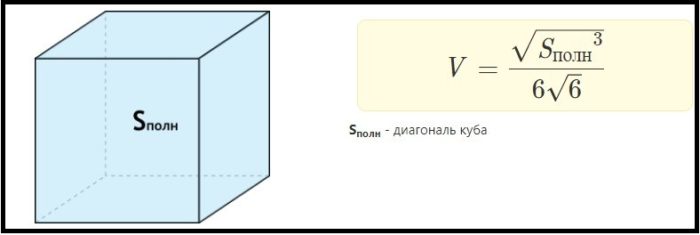
Пример:

Формула вычисления объема конуса

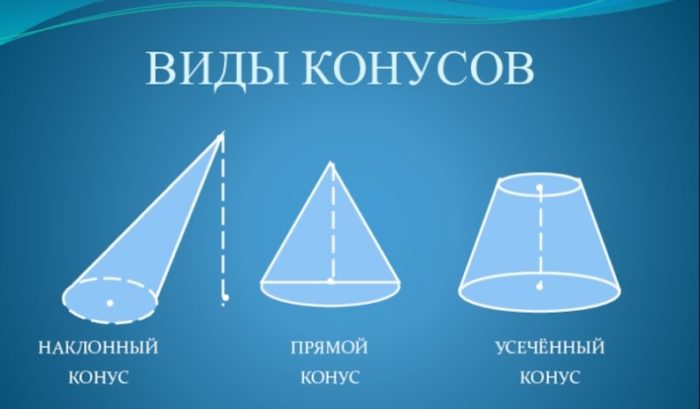
В результате вращения правильного треугольника вокруг катета, в пространстве возникает еще одно тело ― конус. Он является результатом совокупности лучей, которые исходят из вершины конуса и пересекают плоскость.

Объем прямого конуса рассчитывается по формуле:

Пример:

Объем усеченного конуса формула

Когда обычный конус пересекает плоскость, идущая параллельно его основанию, получается усеченный конус. Фигура оказывается между парой плоскостей, поэтому имеет два основания в виде двух кругов разного диаметра. Также у усеченного конуса есть высота, соединяющая основания и идущая перпендикулярно к ним.

Объем такого конуса рассчитывается через радиусы двух его оснований и высоты:

Решение: