Итак, тема сложения и вычитания усвоена, есть четкое представление о математических операциях умножения и деления, можно приступать к делению чисел столбиком. Не каждый школьник с первого урока поймет смысл данной темы, особенно в случаях деления многозначных чисел и чисел с остатком. И здесь ему потребуется всяческая поддержка родителей. Чтобы помочь ребен ;:ку справиться с делением уголком, воспользуйтесь нашими теоретическими подсказками. Статья имеет подробное пояснение хода решения примеров, а также доступные наглядные иллюстрации.
Содержание статьи
- Как научиться делить столбиком 3 класс
- Как научиться делить столбиком 4 класс
- Как научиться делить столбиком на двузначное
- Видео как научиться делить в столбик
- Как научиться делить в столбик с остатком
- Как научиться делить столбиком трехзначные числа
- Как научиться делить в столбик многозначные числа
Как научиться делить столбиком 3 класс
Арифметические расчеты в 3 классе базируются на таблице умножения от 1 до 10 в пределах чисел до 100. На этом этапе ребенок должен понимать сам процесс деления и безошибочно определять категории «делителя», «делимого» и «частного». Конечно, деление многозначных чисел проще всего проводить столбиком. Школьник меньше путается и не теряет цифры. Таким образом, вырабатывается мысленная логическая схема. Суть метода нельзя уловить без знания таблицы умножения и способа «обратного» деления.
Алгоритм деления в столбик:
Например, 98 необходимо разделить в столбик на 7.
В нашем примере 98 – делимое, 7 – делитель, результат деления, который получится в итоге – частное. Его и необходимо найти.
Делимое и делитель запишем рядом, разделив их вертикальной линией с уголком. Теперь необходимо определить, сколько семерок поместится в девятке – одна. Цифру «1» запишем под линией в правом нижнем углу.
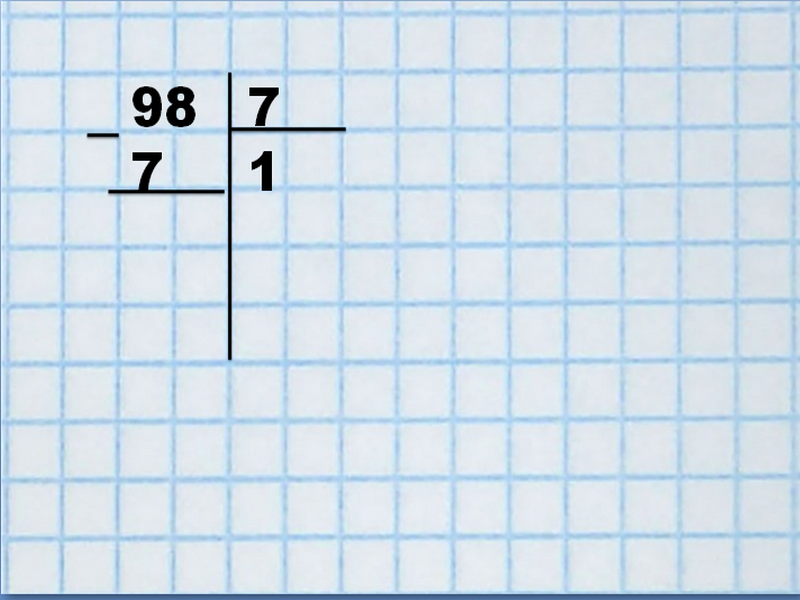
Под девяткой запишем семерку, подчеркнем линией, отнимем и запишем разницу — 2. Если в двойке не помещается ни одной семерки, значит решение верно. Снесем к двойке верхнюю восьмерку. Получим — 28. Проанализируем, сколько семерок может поместиться в цифре «28» – 4. Полученный ответ запишем рядом с «1».
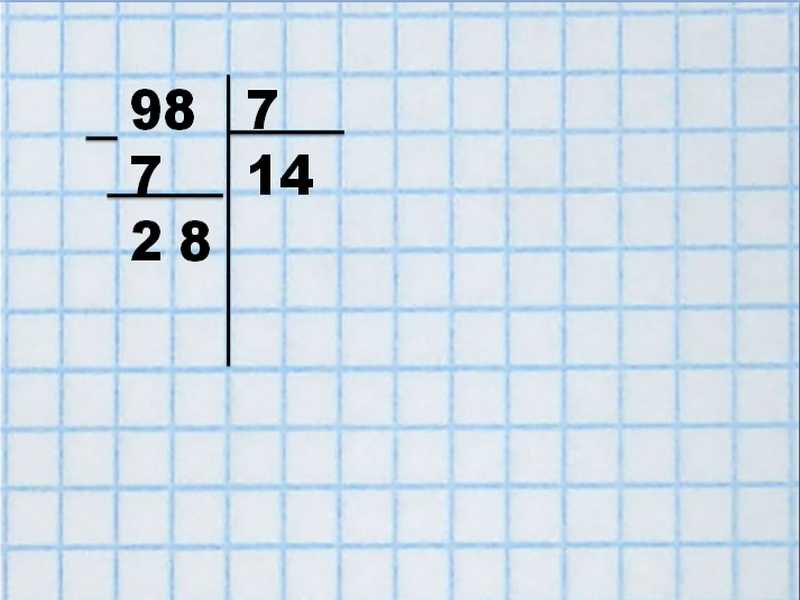
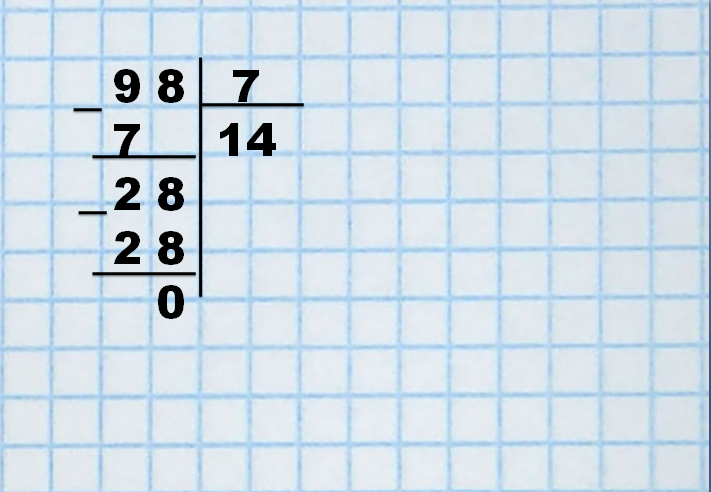
От 28 отнимем цифру «28» и получим «0» — значит, деление произвели правильно. Если в итоге деления не получается ноль, возможна в подсчетах арифметическая ошибка или деление без остатка невозможно. В итоге частное получилось «14».
Правильность деление можно проверить, если при умножении 14 на 7 получается 98 — подсчеты верны.
Главная проблема, с которой сталкиваются третьеклассники на уроках математики – это отсутствие умения производить быстрые арифметические действия. А ведь вся школьная программа начальной школы базируется на этой основе, особенно действия на деление.
Как научиться делить столбиком 4 класс
Программа 4 класса, по сравнению с прошлым учебным годом, усложняется в сторону увеличения расчетных чисел. Четвероклассники проводят деление многозначных чисел больше 100. Они учатся делить уголком числа с двух и трехзначным делителем, а также решать примеры с остатком.
Алгоритм решения деления уголком аналогичен алгоритму, изучаемому в третьем классе.
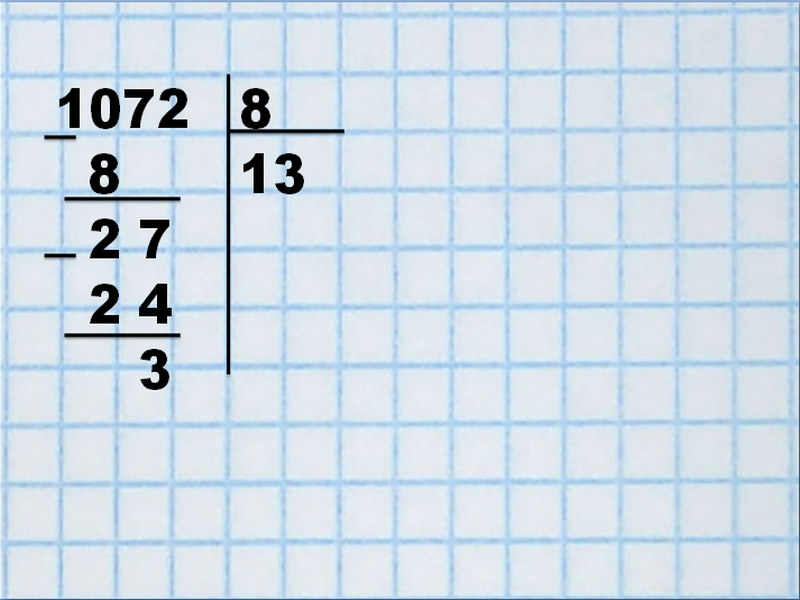
Давайте, в качестве примера 1072 разделим на 8. Сразу необходимо определиться с категориями деления, 1072 — делимое, 8 – делитель. Результат, полученный в качестве действия, — частное.
Числа запишем с двух сторон уголка.
Сразу определимся с числом, которое больше самого делителя. 1<8, поэтому начинают действие с 10. В данном числе может содержаться лишь одна 8. Запишем результат в правой колонке.
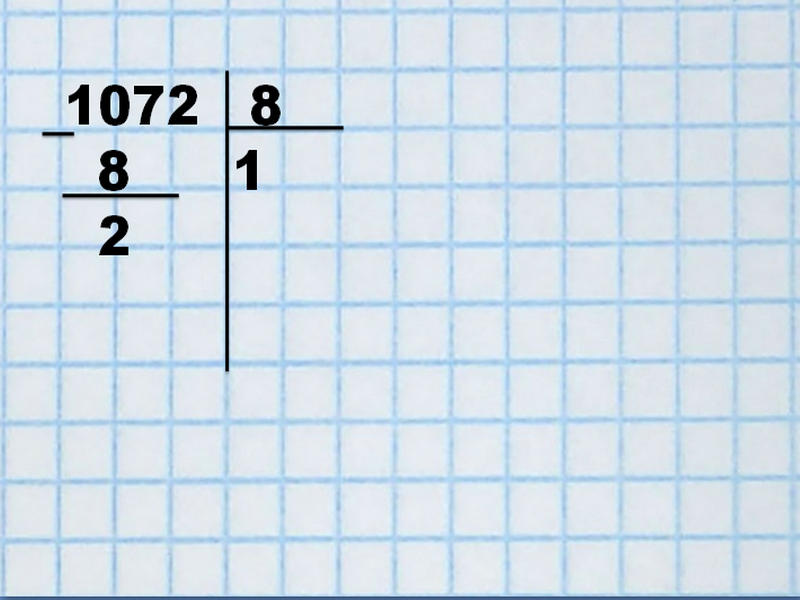
Делитель 8 умножим на 1 и получим — 8. Результат подпишем под делимым 1072 и вычтем. Полученное число 2<8, поэтому его увеличим за счет следующего неиспользованного числа делимого — 7. В итоге получится цифра «27».
Затем действуют по алгоритму. Проанализируем, сколько восьмерок содержит число «27». В нем заключено 3 х 8=24. Цифру «3» допишем в правой колонке рядом с частным 1. На данный момент частное – 13.
Слева от 27 – 24 = 3.
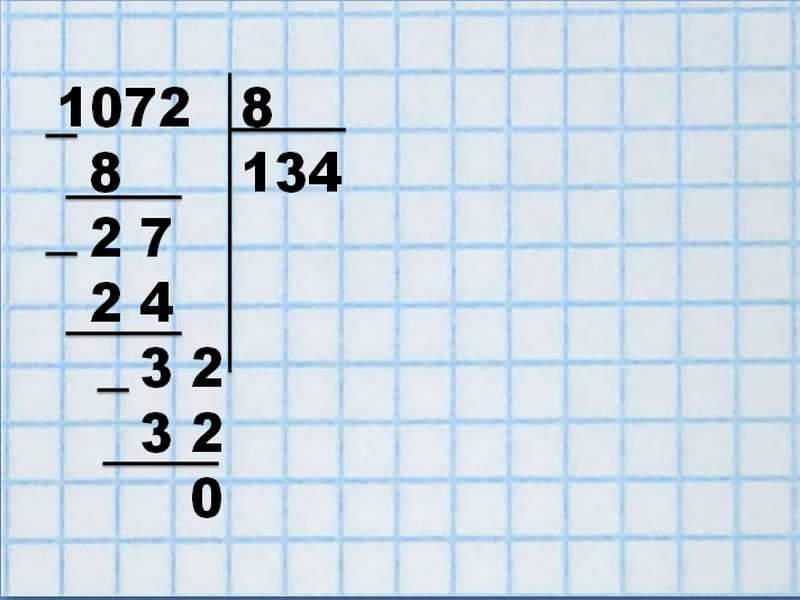
Последним числом частного будет цифра «32», за счет неиспользованного делителя.
Проанализировав число, запишем результат: 32 : 8 = 4. Полученную 4 присоединим к частному — 134. Осталось лишь проверить результат: 134 х 8 =1072.
Как научиться делить столбиком на двузначное
В 4 классе ученик должен уметь делить уголком многозначные значения на двух- и трехзначное число. Полученный навык необходим для дальнейшего курса математики вплоть до 11 класса.
Конечно, такое деление сложнее однозначного, но при правильном подходе и понимании оно не составит труда. Здесь важен правильный подбор чисел и постепенное освоение темы, от простого к сложному.
Для примера выполним действие: 144 : 24
Как и в случае однозначного деления, определим число большее самого делителя: 14<24, т.е. будем делить сразу все число — 144. Прикинем 144 : 20, получим примерно 7. Пробную цифру пока не пишут в колонке. Проверим, 7 х 24 = 168, что значительно больше нашего делимого. Возьмем по 6 х 24 = 144 – это наше число. Подпишем его под делимым и получим ответ – 6.
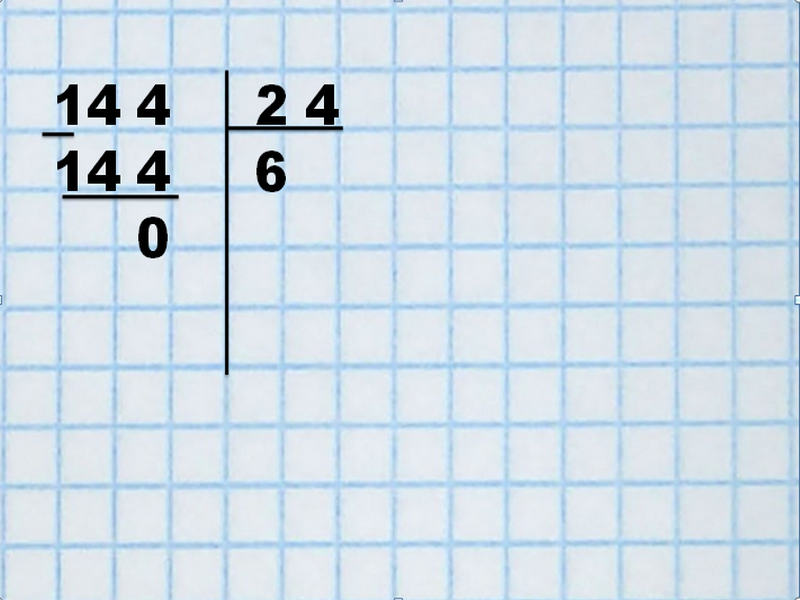
После постепенного освоения простых примеров, можно перейти к более сложным.
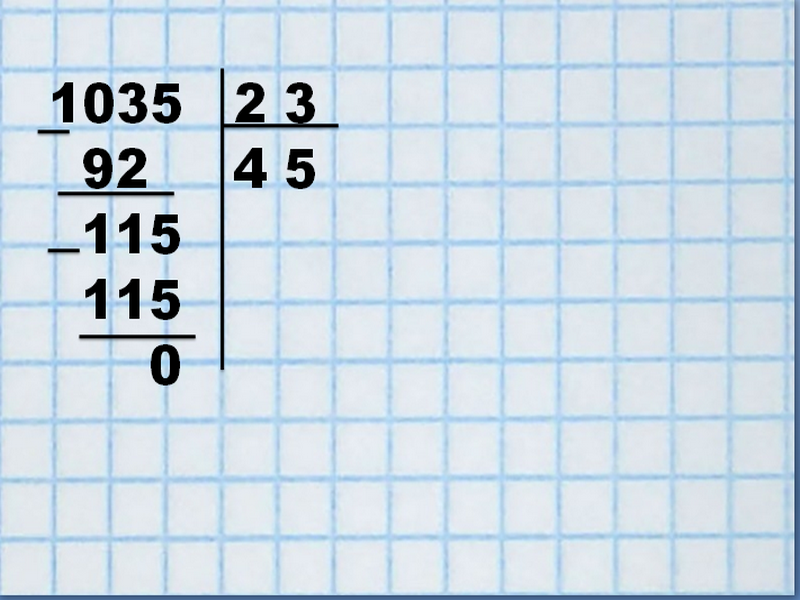
Разделим 1035 на 23.
Определив первую цифру, 103 >23, делим ее на 23. 20 х 5 = 100, но у нас в примере 23 х 5 = 115, что больше 103. Возьмем по 4: 23 х 4 = 92. Запишем ответ в правой колонке под чертой.
От 103 – 92 = 11. Данные запишем под делимым. 11<23, т.е. расчеты сделаны верно.
К 11 снесем 5 и получим цифру «115». Методом подбора определим результат: 23 х 5 = 115.
Цифру «5» запишем рядом с 4 в ответ – 45.
Проверим: 45 х 23 = 1035, результат верен.
Аналогично выполняют деление на любые многозначные числа (трехзначные, четырехзначные и т.п.).
Видео как научиться делить в столбик
Как научиться делить в столбик с остатком
Деление с остатком – следующий этап обучения. Во время таких действий делимое невозможно ровно разделить на части. Ответ примера будет иметь неделимый кусок, меньший делителя. Чтобы школьник быстрее понял смысл математических действий, тему объясняют на доступных примерах.
На подносе находится 34 конфеты, которые нужно разделить на 8 детей. Когда каждый ребенок получит по 4 конфеты, на столе останется еще 2 штуки. Это и будет остаток. Вычисления выглядят следующим образом:
34 : 8= 4 ост (2). Откуда взялась цифра «2»? 8 х 4= 32, 34 — 32= 2.
Принцип деления уголком с остатком аналогичен классическому, с одной разницей – наличием остатка.
Для примера разделим 235 на 14.
235 — делимое, расположим слева, делитель (14) напишем правее. Оба значения между собой разделим уголком. Приступим к поиску целого. 23>14, в данном числе помещается 1 делитель. Единицу запишем внизу под уголком. 23 — 14 = 9.
К 9 снесем 5 — цифру единиц делимого и в итоге получим второе неполное делимое – 95.
Методом подбора разделим 90 : 10 = 9, но в нашем случае 14 х 9= 126, что больше 95.
Попробуем 14 х 8= 112. 112>95, поэтому возьмем на единицу меньше: 7 х 14= 98, что также больше 96 на две единицы. Теперь уже точно известно, что нужная цифра 6: 6 х 14= 84
95 — 84= 11, т.е. 11 — это остаток.
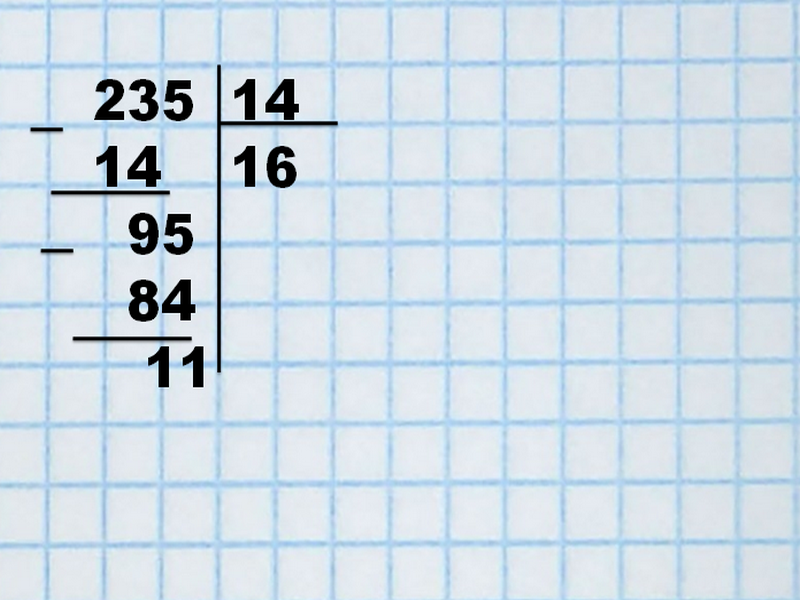
Во время решения примеров с остатком, ответ может быть записан двумя способами:
- в виде дроби, когда в числителе размещают остаток, а в знаменатель записывают делитель:11/16,
- но чаще всего ответ записывают словами: 6 целых и 11 в остатке.
Как научиться делить столбиком трехзначные числа
Когда в делителе стоит трехзначное число, действие лучше всего выполнять в столбик. Алгоритм математического решения аналогичен делению на двузначное число.
Для примера рассмотрим следующие действия: 146676 : 719
146<719, поэтому сразу возьмем четырехзначное число «1466». В данном значении помещается 2 делителя: 719 х 2= 1438. Цифра «2» будет первым значением частного. Ее запишем справа под уголком.
1466 — 1438 = 28. Полученную разность запишем под чертой слева. Снесем к 28 цифру «7». 287<719, поэтому рядом с двойкой запишем «0».
Снесем последнюю цифру делимого «6», в итоге получится число «2876», которое разделим на 719. Возьмем по 3: 719 х 3 = 2157 — мало, можно взять по 4: 719 х 4 = 2876. Цифру «4» запишем рядом с «20», получим в ответе 204. От 2876 отнимем 2876 , получим разность 0.
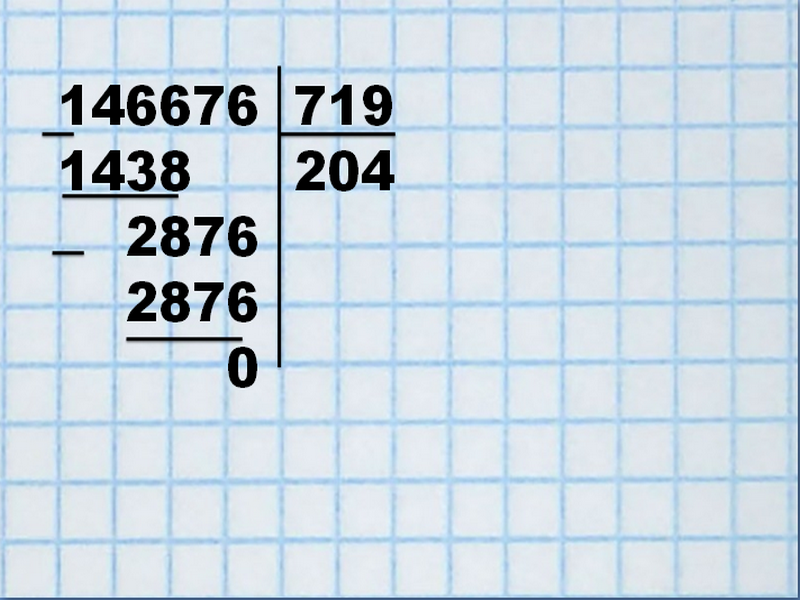
Желательно в конце проверить правильность выполнения действий: 204 х 719 = 146676. Ответ верен.
Как научиться делить в столбик многозначные числа
Этапы деления в столбик многозначного числа аналогичны классическому делению многозначного числа на однозначное. В первом случае учитываем только первую цифру делителя, а при делении на многозначное берем во внимание количество всех цифр делителя. Рабочее число обязательно должно быть больше делителя. В других случаях – добавляем цифру следующего разряда и производим деление по алгоритму.
Математические действия на деление в столбик будут под силу школьнику, если он поймет основной алгоритм вычисления. Правильность решения всегда можно проверить умножением.
